Benchmarking constraint inference in inverse reinforcement learning

abstract

agents unaware of

underlying constraints ← hard to specify mathematically

inverse constrained reinforcement learning (ICRL)

estimates from expert demonstrations

introduction

constrained reinforcement learning (CRL)

learns policy under some known or predefined constraints

not realistic in real-world → hard to specify exact constraints

infer from expert demonstrations

ICRL

infers a constraint function to approximate constraints respected by expert demonstrations

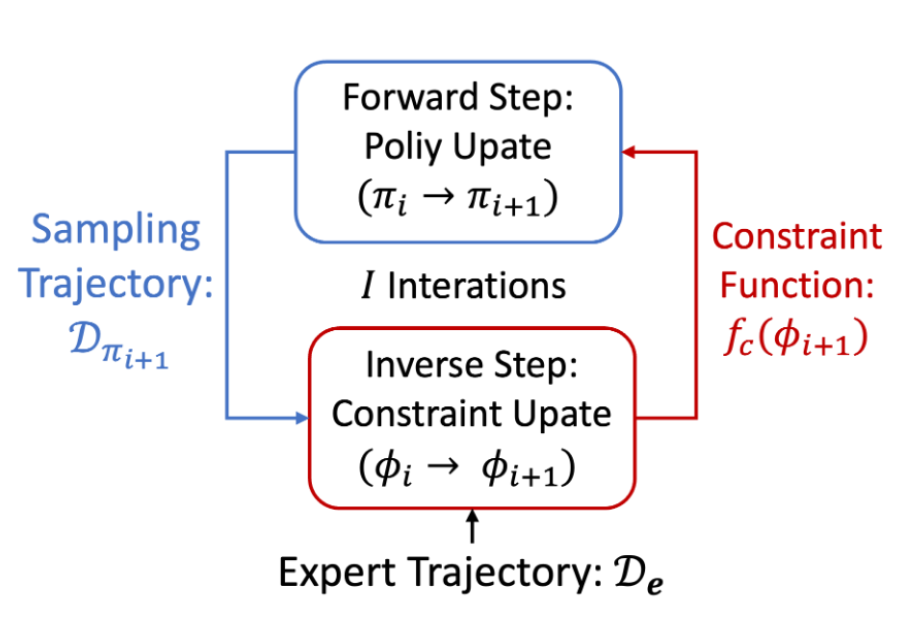
alternating between updating

imitating policy

constraint function

contributions:

1. expert demonstrations might violate constraint
2. under stochastic environment
3. muultiple constraints
4. recovering the exact least constraining constraint

background

constrained reinforcement learning

based on constrained markov decision processes (CMDPs)

to learn policy under cmdp, consider following optimization

cumulative constraints

$\argmax_\pi \mathbb{E}_{p_\mathcal{R}, p_\mathcal{T}, \pi} \left[ \sum^T_{t=0} \gamma^tr_t \right] + \frac{1}{\beta}\mathcal{H}(\pi) \text{ s.t } \mathbb{E}_{p_{\mathcal{c}_i}, p_\mathcal{T}, \pi} \left[ \sum^T_{t=0} \gamma^t c_i(s_t,a_t) \right] \leq \epsilon_i ~{} \forall i \in [0,I]$

where $\mathcal{H}(\pi)$ denotes the policy entropy weighted by $\frac{1}{\beta}$

commonly used in soft setting → recover from undesirable movement i.e. high cost

discounted additive cost less than the threshold

$c_i(s_t,a_t)$

trajectory-based constraints (alternative approach)

defining constraints w/o relying on discounted factor

$\argmax_\pi \mathbb{E}_{p_\mathcal{R},p_\mathbb{T}, \pi} \left[ \sum^T_{t=0}\gamma^tr_t \right] + \frac{1}{\beta} \mathcal{H}(\pi) \text{ s.t. } \mathbb{E}_{\tau \sim (p_\mathcal{T}, \pi), p_{\mathcal{c}_i}}[c_i(\tau)] \leq \epsilon_i ~{} \forall i \in [0,I]$

where $c(\tau)$ is the tracjectory cost

depending on how $c(\tau)$ is defined, we can get more restrictive constraints than cumulative

for example,

$c(\tau) = 1 - \Pi_{(s,a)\in \tau } \phi (s,a)$

where $\phi(s,a)$ indicates the prob

performing a under s is safe

stricter than additive cost

inverse constraint inference

in practice

no constraints but expert demonstrations that follow constraints

goal

agent recover constraint from dataset

challenge

different reward & constraint combination

for identifiability

ICRL assumes rewards are observable

goal

recover the minimum constraint set that best explains expert data

key difference from IRL

IRL learns reward from unconstrained MDP

maximum entropy constrain inference

$p(\mathcal{D}_e | \phi) = \frac{1}{(Z_{\mathcal{M}^{\hat{c}_\phi}})^N} \Phi^N_{i=1} \exp [r(\tau^{i})] \mathbb{1}^{\mathcal{M}^{\hat{c}_\phi}}(\tau^{(i)})$

where

1. $N$ denotes # of trajectories in the demonstration dataset $\mathcal{D}_e$
2. normalizing term $Z_{\mathcal{M}^{\hat{c}_\phi}} = \int \exp [r(\tau)] \mathbb{1}^{\mathcal{M}^{\hat{c}_\phi}} (\tau) \text{d} \tau$
3. indicator $1^{\mathcal{M}^{\hat{c}_\phi}}(\tau^{(i)})$. can be defined by $\phi(\tau^{(i)}) = \Pi^T_{t=1} \phi_t$ and $\phi_t(s_t^i,a_t^i)$ defines to what extent the trajectory $\tau^{(i)}$ is feasible

$\nabla_\theta \log[p(\mathcal{D}_e|\phi)] = \sum^N_{i=1} [\nabla_\phi \sum^T_{t=0} \log\left[\phi_\theta(s_t^{(i)},a_t^{(i)})]\right] - N \mathbb{E}_{\hat{\tau}\sim \pi_{\mathcal{M}^\phi}}\left[ \nabla_\theta \sum^T_{t=0} \log[\phi_\theta(\hat{s}_t, \hat{a}_t] \right]$

ICRL can be formulated as a bi-level optimization problem that iteratively updates

upper-level objective

policy optimization

lower-level objective

constraint learning until convergence

$\pi$ matches expert policy