Multi-Modal Inverse Constrained Reinforcement Learning from a Mixture of Demonstrations

abstract

inverse constraint reinforcement learning (icrl)

recover the underlying constraints

existing algorithms assume single type of agent

challenging to explain why unified constraint function

multi-modal inverse constrained reinforcement learning (MMICRL)

different types of experts

flow-based density estimator

unsupervised expert identification

novel multi-modal constrained policy optimization

minimizes agent-conditioned policy entropy

maximizes the unconditioned one

contrastive learning framework ← enhance robustness

capture diversity

introduction

problematic to leverage one single constraint model

previously to differentiate expert demonstrations

inferred the latent structure of expert demonstrations

identified by behavioral preferences

no theoretical guarantee that optimal model is identifiable

contributions

1. unsupervised agent identification

   flow-based density estimator

   each agent’s policy must correspond to a unique occupancy measure

2. agent-specific constraint inference

   using the identified demonstrations

   estimates a permissibility function → construct constraints for each type of agent

3. multi-modal policy optimization

   comparing the similarity between

   expert trajectories

   generated ones by imitation policies under inferred constraints

   treat generated trajectories as

   noisy embeddings of agents

   enhance similarity between embeddings for agents of the same type

problem definition

constrained mixture-agent markov decision process

CMA-MDP $\mathcal{M}^\phi$

$(\mathcal{S}, \mathcal{A}, \mathcal{Z}, \text{R}, p_\mathcal{\tau}, \{(p_{\mathcal{c}_i}, \epsilon_i) \}_{\forall i}, \gamma, \mu_0)$

$\mathcal{Z}$ denotes the latent code (for specifying expert agents)

in contrast to multi-agent reinforcement learning (MARL)

multiple agents act concurrently

do not distinguish agent types, policies, and constraints

cma-mdp allows

only one agent to operate at a given time

policy update under conditional constraints

constrained reinforcement learning (CRL)

goal → max reward under conditional constraints

$\mathcal{J}(\pi | z) = \max_\pi \mathbb{E}_{\mu_0, p_\tau, \pi} \left[ \sum^T_{t=0} \gamma^tr_t \right] + \beta \mathcal{H}(\pi) \\ \text{ s.t. } \mathbb{E}_{\tau \sim (\mu_o, p_\tau, \pi), p_{\mathcal{c}_j}}\left[ c_j(\tau|z)\right] \leq \epsilon_j(z) ~{} \forall j \in [0, J]$

where

$\mathcal{H} (\pi)$ denotes policy entropy weighted by $\beta$

$c(\tau | z) = 1 - \Pi_(s,a)\in \tau \phi(s,a|z)$ denotes trajectory cost

$\phi(s,a|z)$ denotes permissibility function that indicates the prob. performing action $a$ under state $s$ is safe for agent $z$

assumes constraints are known

instead, we only have

expert demonstrations that follow the underlying constraints

therefore, agents must recover the constraints

constraint inference from a mixture of expert dataset

$p(\mathcal{D}_E|\phi) = \frac{1}{Z_{\mathcal{M}^{\hat{c}_{\phi}}}} \Pi^N_{i=1} \sum_z \mathbb{1}_{\tau^i \in \mathcal{D}_z} \exp [r(\tau^{(i)})] 1^{\mathcal{M}^{\hat{c}_\phi}}(\tau^{(i)}|z)$

where

$N$ denotes # of trajectories in the demonstration dataset

$Z_{\mathcal{M}^{\hat{c}_\phi}}$ denotes a normalizing term

$1^{\mathcal{M}^{\hat{c}_\phi}}(\tau^{(i)})$ denotes permissibility indicator and can be defined by

$\phi(\tau^{(i)}|z) = \Pi^T_{t=1} \phi_t(s^i_t,a^i_t | z)$

$1_{\tau^{(i)}\in \mathcal{D}_z}$ denotes whether the trajectory $\tau^{(i)}$ is generated by the agent $z$ (agent identifier)

icrl for a mixture of experts

mmicrl

1. exhibit high entropy when agent type is unknown

2. collapse to a specific behavioral mode when type is determined

   low entry when agent type is known

$\text{Minimize} ~{}~{} -\alpha_1\mathcal{H}[\pi(\tau)] + \alpha_2 \mathcal{H}[\pi(\tau|z)] \\ \text{Subject to} ~{} \begin{aligned} &\int\pi(\tau|z)f_z(\tau)\text{d}\tau = \frac{1}{N} \sum_{\tau\in \mathcal{D}_z}f(\tau) \\ &\int \pi(\tau|z)\text{d}\tau = 1 \\ & \int \pi(\tau|z)\log \phi(\tau|z)\text{d}\tau \geq \epsilon \end{aligned}$

where

$f(\cdot)$ denotes a latent feature extractor

objective differs from traditional maximum entropy rl in two ways

1. minimizes an entropy conditioned on agent types
2. additional constraint related to policy permissibilty

Proposition LET $p(z|\tau)$ denote the trajectory-level agent identifier, let $r(\tau) = \frac{\lambda_0}{\alpha_2 - \alpha_1} f(\tau)$ denote the trajectory rewards, let $Z_{\mathcal{M}^{\hat{c}_\phi}}$ denote a normalizing term. The optimal policy of the above optimization problem can be represented as

$\pi(\tau|z) = \frac{1}{Z_{\mathcal{M}^{\hat{c}_\phi}}} \exp \left[ \frac{\alpha_1 \mathbb{E}_{z \sim p(z)} [\log(p(z | \tau))]}{\alpha_2 - \alpha_1} + r(\tau) \right] \phi(\tau | z)^{\frac{\lambda_2}{\alpha_1 - \alpha_2}}$

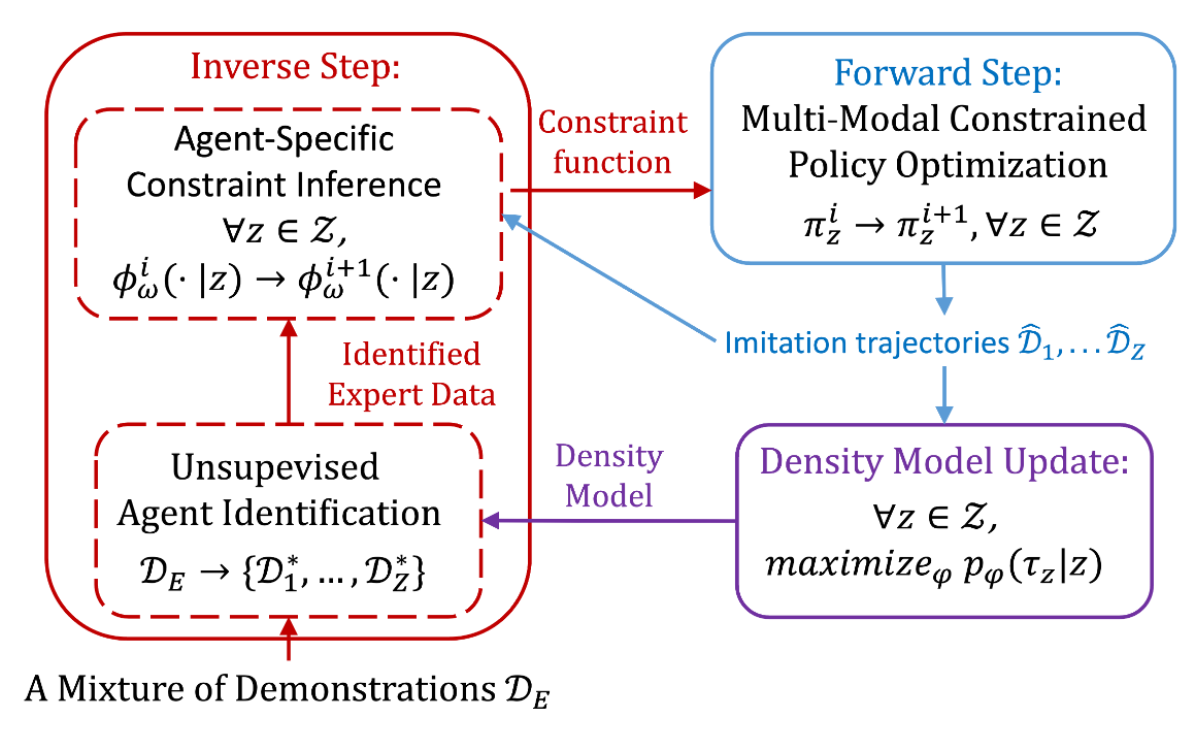
kep iterative steps of mmicrl

1. unsupervised agent identification for calculating $p(z|\tau)$
2. conditional inverse constraint inference for deducing $\phi(\tau | z)$
3. multi-modal policy update for approximating $\pi(\tau|z)$

mmicrl alternates between these steps until

imitation policies reproduce expert trajectories

question: what if expert trajectories violates the underlying constraints as well?

unsupervised agent identification

mmicrl performs

trajectory level agent identification

state action density

$\rho_\pi(s,a) = (1 - \gamma)\pi(a|s) \sum^\infty_{t=0} \gamma^t p(s_t = s | \pi)$ where $p(s_t = s | \pi)$ is the probability density of state $s$ at time step $t$ following policy $\pi$

Proposition 4.2. Suppose $\rho$ is the occupancy measure tha satisfies the Bellman flow constraints: $\sum_a \rho(s,a) = \mu_0(s) + \gamma \sum_{s^\prime,a} \rho(s^\prime,a) P_\tau (s^\prime|s,a)$ and $\rho(s,a) \geq 0$. Let the policy defined by $\pi_\rho (a | s) = \frac{\rho(s,a)}{\int \rho(s,a^\prime)\text{d}a^\prime}$, then $\pi_\rho$ is the only policy whose occupancy measure is $\rho$.

Bellman Flow Constraint is defined as

$\mathcal{\chi}(s,a) = \pi(a|s) \cdot [(1 - \gamma) \mu_0(s) + \gamma \int \chi(s^\prime, a^\prime) \tau(s|s^\prime, a^\prime)\text{d}s^\prime d^\prime]; \quad \chi(s,a) \geq 0$

It can be shown that occupancy measure $\rho^\pi(s,a)$ is a unique solution to Bellman flow constraint

Density Estimation

“one can identify an expert agent by examining the occupancy measures in the expert trajectories”

conditional Flow-based Density Estimator (CFDE)

extimates the density of input variables in the training data distribution under an auto-regressive constraint

conditions on agent types

the function $\psi$ is implemented by stacking multiple MADE layers

$p(x_i | x_{1:i-1}, z) n= \mathcal{N}(x_i|\mu_i, (\exp(\alpha_i))^2) \\ \text{ where } \mu_i = \psi_{\mu_i} (x_{1:i-1}, z) \text{ and } \alpha_i = \psi_{\alpha_i} (x_{1:i-1}, z) \\ \\$

$p_\psi(z|\tau) = \frac{\Pi_{(s,a)\in\tau}p_\psi(s,a|z)}{\sum_{z^\prime} \Pi_{(s,a)\in\tau} p_\psi(s,a|z^\prime)}$

Agent Identification

add $\tau^i$ to $\mathcal{D}_z$ if $z = \argmax_z \sum_{(s,a)\in\tau_i} \log[p_\psi(s,a|z)]$

agent-specific constraint inference

$\nabla_\omega\log[p(\mathcal{D}_z|\phi,z)] \coloneqq \sum^N_{i=1} [\nabla_\phi \sum^T{t=0} \eta \log[\phi_\omega (s^{(i)}_t, a^{(i)}_t |z)]] - N \mathbb{E}_{\hat{\tau}\sim\pi_{\mathcal{M}^\phi}(\cdot|z)} [\nabla_\phi \sum^T_{t=0}[\eta \log [\phi_\omega \hat{s}_t, \hat{a}_t |z)]]$

multi-modal policy optimization

the multi-modal policy optimization object

$\min_\pi -\mathbb{E}_{\pi(\cdot|z)} \left[ \sum^T_{t=1} m\gamma^t r(s_t, a_t) \right] - \alpha_1 \mathcal{H}[\pi(\tau)] + \alpha_2 \mathcal{H}[\pi(\tau|z)] \\ \text{s.t. } \mathbb{E}_{\pi(\cdot|z)} \left( \sum^h_{t=0} \gamma^t \log \phi_\omega(s,a,z)\right) \geq \epsilon$

learning diverse policies via contrastive estimation

directly augmenting rewards lead to sub-optimal policy

a large penalty to trajectories with log $p_\psi(z|\tau)$

more sensitive to dense estimation rather than reward signals

replace the identification probability with a contrastive estimation method

$\min_\pi -\mathbb{E}_{\pi(\cdot|z)} \left( r(\tau) + \alpha_1 L_{ce} (\tau, \mathcal{V}_{1, \dots, |Z|} ) \right)+ (\alpha_2 - \alpha_1) \mathcal{H}(\pi(\tau|z)) \\ \text{ s.t. } \mathbb{E}_{\pi(\cdot|z)} \left( \sum^h_{t=0} \gamma^t \log \phi_\omega (s,a,z)\right) \geq\epsilon$

where $\mathcal{Z}$ is the probing sets

using sets generated by CFDE

$L_{ce}(\tau, \mathcal{V}_{1, \dots, |Z|} ) = \sum^T_{t=0} \log \frac{\exp \left[ \sum_{(\hat{s}_z, \hat{a}_z) \in \mathcal{V}_z} f_s[(s_t, a_t), (\hat{s}_t, \hat{a}_t)] \right]}{\sum_{\tilde{z} \in \mathcal{Z}} \exp \left[ \sum_{(\hat{a}, \hat{a}) \in \mathcal{V}_{\tilde{z}}} f_s[(s_t,a_t),(\hat{s},\hat{a})]\right]}$

where $f_s$ denotes the score function for measuring the similarity between different state-action pairs using cosine similarity

$(s,a) \in \{\tau, \mathcal{V}_z\}$ → positive embeddings for $\pi(\cdot | z)$

$(\tilde{s}, \tilde{a}) \in \{\mathcal{V}_{\tilde{z}}\}_{\tilde{z} \neq z}$ → negative embeddings for $\pi(\cdot | z)$

consider generation as injecting environmental noise into the policy

since $\mathcal{V}_z$ belongs to high-conditional density region in $p(\cdot|z)$

knowledge from density estimator is integrated into policy updates